論理とは何か?
よく論理的に話せとか、論理的に考えろなどと言う方がいらっしゃいますが、そういう方はひとまず置いておいて、数学やコンピューターサイエンスの観点から論理とは何かをお話ししたいと思います。
論理とは必ず答え(結果)が、「はい」か「いいえ」になることを言います。
論理演算と論理式
コンピューターでは様々な計算を行っていますが、それを論理演算として行っています。論理演算では、「はい」は「TRUE(真)」「いいえ」は「FALSE(偽)」と表します。論理演算では「TRUE」は「1」は「FALSE」は「0」と表すこともあります。
| TRUE | 真 | 1 | Yes | はい |
| FALSE | 偽 | 0 | No | いいえ |
その論理演算を行うための式が論理式です。以下は論理式の簡単な例です。(※記号 == は両辺が等しいことを表すものとします。)
x == 0
変数xにどんな値が入っても必ず、答え(結果)が「TRUE」か「FALSE」になります。例えばxが0ならこの式は成り立つので、「TRUE」。xが0以外ならこの式は成り立たないので、「FALSE」となります。
コンピューターはプログラムで動きますが、そのプログラム自体が大きな論理式であると言えます。
2進数とbit(ビット)
ではなぜコンピューターを動かすプログラムが論理式である必要があるのでしょうか?
コンピューターは「0」か「1」で計算していると聞いたことはありますか?これをさらに具体的に言うと、コンピューターは2進数で計算を行っています。私たちが普段用いているのは10進数です。10進数では、9の次は10となり桁が1つ増えます。一方2進数では、1の次はもう桁上がりして10となります。
| 2進数(2で桁上がり) | 10進数(10で桁上がり) |
| 0 | 0 |
| 1 | 1 |
| 10(←桁上がり) | 2 |
| 11 | 3 |
| 100(←桁上がり) | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000(←桁上がり) | 8 |
| 1001 | 9 |
| 1010 | 10(←桁上がり) |
2進数では、あらゆる数値(データ)を「0」と「1」だけで表すことができるのです。この「0」か「1」どちらかになる2進数の1桁をbit(ビット)と言います。以下の図は珠が1つしかないそろばんです。そろばんの珠が下がっているときが「0」、上がっているときが「1」です。このそろばんの1桁が1bitで、8桁つまり8bitで1byte(バイト)です。byteはデータの容量などでよく使われている単位ですね。
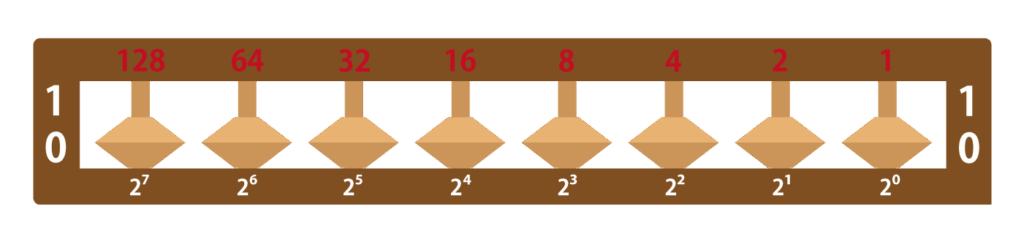
1byteでは0から255までの数値(データ)を表せます。2進数のn桁目の値は、2n-1です。例えば、3桁目なら23-1で、4です。ちなみに10進数ならn桁目の値は10n-1です。例えば3桁目なら103-1で100になります。各桁の値をすべてを足し合わせるので、例えば1Byteそろばんの1桁目と3桁目の珠が上がっていれば、101。これを10進数になおすと、1+4で5になります。
| n桁目 | 2n-1 | 10n-1 |
| 1 | 20 (1) | 100 (1) |
| 2 | 21 (2) | 101 (10) |
| 3 | 22 (4) | 102 (100) |
| 4 | 23 (8) | 103 (1,000) |
| 5 | 24 (16) | 104 (10,000) |
| 6 | 25 (32) | 105 (100,000) |
| 7 | 26 (64) | 106 (1,000,000) |
| 8 | 27 (128) | 107 (10,000,000) |
上記のようにコンピューターは、「0」と「1」の組み合わせでデータを表現しているため、コンピューターを動かすプログラムは論理式、つまり結果が必ず「FALSE(0)」か「TRUE(1)」になる式でないといけないのです。








